Question

Round your ar(s) to the nearest hundredth. (If there is more than one answer, use the "or" button.)Find all values of t for which the ball's height is 12 meters.A ball is thrown from an initial height of 2 meters with an initial upward velocity of 25m / s The ball's height h (in meters) after t seconds is given by thefollowing.h = 2 + 25t - 5t ^ 2

Answer 1

From the question, the ball's height in meters is represented by the equation

`h=2+25t-5t^2​`

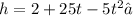
Now we are told to find all values of t, for which the ball's height is 12 meters.

This means that h = 12 meters.

So that means

`\begin{gathered} h=2+25t-5t^2​=12 \\ So\text{ we have } \\ 12=2+25t-5t^2​ \\ 2+25t-5t^2​=12 \\ -5t^2​+25t+2-12=0 \\ -5t^2​+25t-10=0 \\ \text{ multiplying by minus sign we have } \\ -(-5t^2​+25t-10=0 \\ 5t^2​-25t+10=0 \\ \text{dividing through by 5 we have } \\ t^2-5t+2=0 \end{gathered}`

So now solving the quadratic equation for t, we have

`\begin{gathered} t^2-5t+2=0 \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{Where a = 1, b = -5, c =2 } \\ t=\frac{-(-5\pm\sqrt[]{(-5)^2-4*1*2}}{2*1} \\ t=\frac{5\pm\sqrt[]{17}}{2} \end{gathered}`

So, either

`\begin{gathered} t=\frac{5+\sqrt[]{17}}{2} \\ t=4.56155281 \\ t=4.56\sec s \end{gathered}`

Or

`\begin{gathered} t=\frac{5-\sqrt[]{17}}{2} \\ t=0.43844718 \\ t=0.44\sec s\text{ } \end{gathered}`

Hence the answer is t = 4.56 secs or 0.44 secs