26.67
Step-by-step explanation
Step 1
let´s find the equations to solve:
a ratio is a relationship between two quantities, normally expressed as the quotient
so
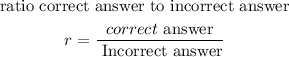
we are told that the raio for lesly was 8, hence

a)
if we let
number of correct answers = x
number of incorrect answers = y
we would have

b) if the total of question is 30,then
total questions= total anwers= correct answer +incorrect answer
replace
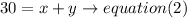
Step 2
solve the equations
a) isolate the x value from equation (2) and replace in equation (1)
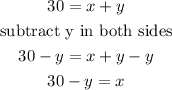
replace the x value in equation(1)
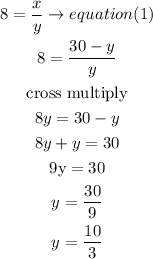
replace the y value in equation (2)
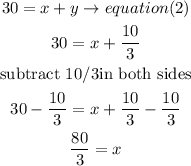
so, the total of correct answer is x
x=80/3= 26.67
the numbers of correct answer is 26.67
I hope this helps you