Answer:
cos (A + B) = - 57 / 185
Explanation:
First we draw the triangle containing angle A
From the above, we find that the length of the hypotenuse is 5; therefore,
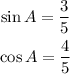
Now we draw the triangle containing angle B.
The length of the vertical side from Pythagoras's theorem is 35; therefore,
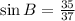
Now,
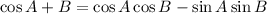
Putting in the values of cos A, cos B, sin A, and sin B we found above gives
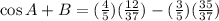

which is our answer!