The given functions are
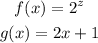
First, we have to find the composite function
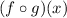
We have to enter g(x) inside f(x), as follows
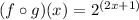
Now, we evaluate this composition when x = 0.
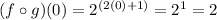
Therefore, the evaluation of the first case gives 2.
Now, we find the second composition, this time we have to enter f(x) inside g(x).
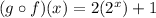
We evaluate the composition when x = 2.
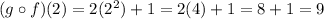
Therefore, the evaluation of the second case gives 9.