Question

can someone else try and do this, I did it twice in the first time I got 9.8 and then the second time I got 17.4 and I don't think either of those all right

Answer 1

We have 3 lines and one pair of it, DE and GH are parallel.

We have to find the value of x that satisfy that condition.

If we draw only these lines, we can relate the angles as:

If DE and GH are parallel, then the angle at H, with measure (5x+22), and the angle at D, with measure still to be calculated, are alternate interior angles and therefore have the same measure.

We can calculate the measure of the angle at D using the fact that the sum of the measures of the interior angles of a triangle is equal to 180 degrees.

Then, for triangle DEF, we can write:

`\begin{gathered} m\angle D+m\angle E+m\angle F=180 \\ m\angle D+71+42=180 \\ m\angle D=180-71-42 \\ m\angle D=67 \end{gathered}`

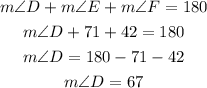
Now that we know the measure of D, we can write:

`\begin{gathered} m\angle H=m\angle D \\ 5x+22=67 \\ 5x=67-22 \\ 5x=45 \\ x=(45)/(5) \\ x=9 \end{gathered}`

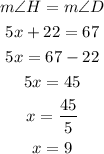
Answer: the value of x is x=9.