An odd function is a function that satisfies:
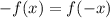
If f(x) is an odd function, we can try with to see if each of the options to see if they are odd functions:
a) In the case of the absolute function, it can not be an odd function, as it will always be positive for all x.
b) f(x-1) is a translation of f(x) to the right. If f(x) is an odd function, f(x-1) will not be neither an odd function or an even function, as it will not have symmetry respect to the origin.
c) -f(x) will change the sign of f(x), so it will have the same symmetry respect to the origin but rotated 180° from f(x). Then, it is still an odd function.
d) f(|x|) will not have the same symmetry properties of f(x) so it will not be an odd function.
Answer: - f(x) [Option C]