Question

The bar graph to the right shows the average number of hours of people sleep per day, by age group. Use this information to complete part B

Answer 1

`\text{The relation is }\lbrace(9.3,18),(9.1,21),(8.6,30),(8.9,45),(8.4,50),(8.2,65)\rbrace`

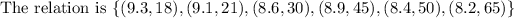
Explanations:

Given the coordinate that represents the ordered pair of the function expressed as:

`f=\mleft\lbrace(18,9.3),(21,9.1),(30,8.6),(45,8.9),(50,8.4),(65,8.2)\mright\rbrace`

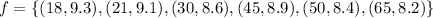
The set of the inverse of the function will be determined by simply switching the coordinates of the function. The inverse function rule is described as:

`(x,y)\rightarrow(y,x)`

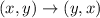
Applying this rule, the inverse of the set of ordered pairs will be given as:

`f^(-1)(x)=\lbrace(9.3,18),(9.1,21),(8.6,30),(8.9,45),(8.4,50),(8.2,65)\rbrace`

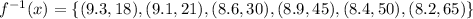
This gives the relation of its inverse function.