First, let's remember what the axis of symmetry means.
The axis of symmetry is a line that splits our parabola in half. This line also has a very interesting property: The vertex belongs to this line.
(illustrative example. Not the given parabola)
Now, for the particular parabola we're given, we know that this axis of symmetry is:
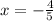
Notice that, taking into account what we already know about the defnition of the axis of symmetry, we can conclude that this is the x-coordinate of the vertex.
To find the corresponding y-value, we just plug it in the formula of our parabola:
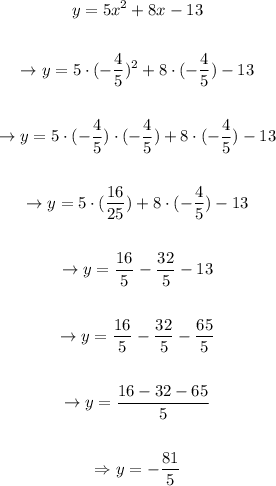
Therefore, we can conclude that the y-coordinate of our vertex is:

(Given parabola, with its axis of symmetry and vertex highlighted)