1 Answer

GeneSummons · Answer 1 · 2023-09-10T23:31:52+0000

Let us begin by defining the formula for calculating probability of an event occuring:

$P(an\text{ event occuring) = }\frac{Number\text{ of times the event occured}}{Total\text{ number of trials}}$

Before we proceed, let us enumerate the given variables

121 people walked by the store

52 came into the store

29 bought something

(a) The probability that a person who walked by the store would come into the store:

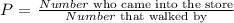
$P\text{ = }\frac{Number\text{ who came into the store}}{Number\text{ that walked by}}$

Substituting we have:

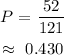
$\begin{gathered} P\text{ = }(52)/(121) \\ \approx\text{ 0.430} \end{gathered}$

Answer: 0.430

(b) The probability that a person who enters the store will buy something

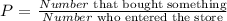
$P\text{ = }\frac{Number\text{ that bought something}}{Number\text{ who entered the store}}$

Substituting we have:

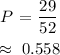
$\begin{gathered} P\text{ = }(29)/(52) \\ \approx\text{ 0.558} \end{gathered}$

Answer: 0.558

(c) The probability that a person who walks by the store will buy something

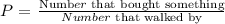
$P\text{ = }\frac{\text{Numb}er\text{ that bought something}}{Number\text{ that walked by}}$

Substituting we have:

$\begin{gathered} P\text{ = }(29)/(121) \\ \approx\text{ 0.240 } \end{gathered}$

Answer: 0.240

(d) The probability that a person who comes into the store will buy nothing

To calculate this, we use the formula:

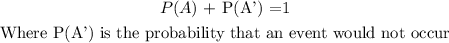
$\begin{gathered} P(A)\text{ + P(A') =1} \\ \text{Where P(A') is the probability that an event would not occur} \end{gathered}$

The probability that a person who comes into the store would buy something is 0.558

Hence:

$\begin{gathered} P\text{ = 1 - 0.558} \\ =\text{ 0.442} \end{gathered}$

Answer: 0.442

Please log in or register to add a comment.