Given the function:
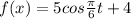
The t is the number of hours after midnight.
Let's estimate how many hours elapse between the first two times the buoy is exactly 6 m above sea level.
We have:
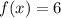
Substitute 6 for f(x) and solve for t.
We have:
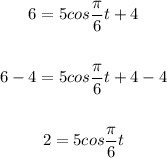
Divide both sides by 5:
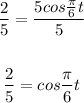
Take the cos inverse of both sides:
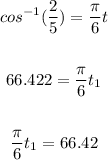
Also, the second angle is:
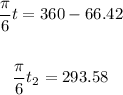
Now, let's solve both equations for t:
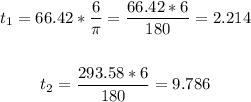
First time = 2.214 hours
Second time = 9.786 hours
Now, to solve for the time, t, we have:
t = t2 - t1 = 9.786 - 2.214 = 7.575 ≈ 7.6 hours.
Therefore, 7.6 hours elapsed between the first two times the buoy is 6m above sea level.
ANSWER:
D. 7.6 hours.