The measure of an exterior angle in a polygon with n sides is given by:

So, for n = 20, we have the measure of the exterior angles of the polygon with 20 sides:

Now, to find the sum of all exterior angles, let's multiply the exterior angles by the number of sides of the polygon:
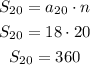
Therefore the sum is equal to 360°, correct option: B.
(The sum of exterior angles of a polygon with n sides is always equal to 360°)