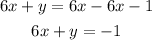Question

Which equation represents a line which is perpendicular to the line y = 5x – 1?

Answer 1

6x + y = -1

Step-by-step explanation:

The general slope-intercept form of the equation of a line is given as;

`y=mx+b`

where m = slope of the line

b = y-intercept

Given the below equation of a line;

`y=(1)/(6)x-1`

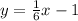
we can see that the slope of the line, m = 1/6 and the y-intercept, b = -1

Any line that will be perpendicular to the above line must have a negative reciprocal of its slope. So if the slope of the given line is 1/6, then the slope of the perpendicular line will be;

`-(1)/(((1)/(6)))=-1\ast(6)/(1)=-6`

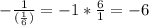
So the slope of the perpendicular is -6, the equation of the line can then be written as;

`\begin{gathered} y=-6x-1 \\ \end{gathered}`

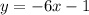
Looking at the given options in the question, we'll need to rewrite the above equation;

Let's add 6x to both sides of the equation, we'll have;

`\begin{gathered} 6x+y=6x-6x-1 \\ 6x+y=-1 \end{gathered}`