The equation of line passing through the points is given by,
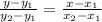
Let,
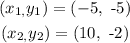
Then the equation of the line is,
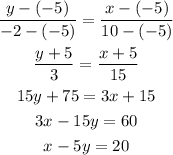
Converting the above equation into the intercept form,
Dividing the equation on both sides by 20,
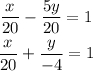
On comparing the above equation with the intercept form
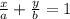
We get,
x-intercept is, a=20 and the y-intercept is, b=-4