We have two cases:
Sale: transation is positive and the 1.5% is charged. So, the interval for this is x positive, that is:
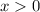
And the amount charged will be 1.5% of x, so:
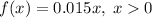
Returns: transaction is negative and 0.5% is charged. Notice that it doesn't say it returns 0.5%, so Isabel has to pay the 0.5%, so the end value will be positive.
The interval is for x negative, so:
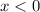
And since the final amount is charged from Isabel, we can't use the negative value, because this would mean she is charged a negative value. Thus, we need to change the sign of x by using a negative sign and then apply the 0.5%:
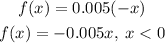
Now, we have to deal with x = 0, however, notice that in both cases if we input x = 0 we will have f(0) = 0. Also, this makes sence, because if x = 0 this means we have either a return of 0 or a sale of zero, which shoule be charged 0.
This means that we can introduce x = 0 to either parts. Let's do it on the sales part.
So, in the end we have:
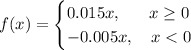
To graph the function, we will need the point where they change from one to the other and, since they both are linear functions, we will need one more point on each.
The point in which they meet we already saw, it is x = 0 and on both parts f(0) will be 0, so on both lines we have (0, 0).
Now, we can pick one point to the left of that and one to the right, which can be x = -100 and x = 100:

So, we have points (-100, 0.50) and (100, 1.50). Ploting the points and the graphing the lines, we have: