Question

If r varies jointly as s and t and inversely as u, and r =18 when s=2, t=3, and u =4, find s when r=6, t=2, and u=4

Answer 1

To find the value of s, we must first set up the equation so that we can get the coefficient of variation. Based on the given, the equation is:

`r=k(st)/(u)`

Let's substitute the given values of r, s, t, and u to solve for k.

`\begin{gathered} r=k(st)/(u) \\ \\ 18=k((2*3)/(4)) \\ \\ 18=k((3)/(2)) \\ \\ k=18((2)/(3)) \\ \\ k=12 \end{gathered}`

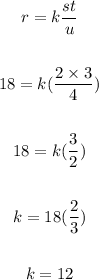
Now that we know k = 12, we can solve for s.

`\begin{gathered} r=k(st)/(u) \\ \\ 6=12((s*2)/(4)) \\ \\ 6=6s \\ \\ s=1 \end{gathered}`

The answer is: s = 1.