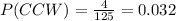Question

multiple choice questions each have five possible answers A B C D or e one of which is correct assume that you guessed the answers to three such questions use the multiplication rule to find ( p c c w) where C denotes a correct answer and w denotes a wrong answer

Answer 1

The questions have 5 options, and only one of those options is correct and four of those options are wrong.

Before we answer the question, we need to calculate two probabilities:

• the probability of getting a correct answer

,

• the probability of getting a wrong answer

To calculate these probabilities, we use the probability formula:

`P(x)=\frac{\text{Number of favorable outcomes}}{total\text{ number of outcomes}}`

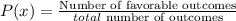
For the probability of getting a correct answer the number of favorable outcomes is 1 because only one is the correct option, and the total number of outcomes is 5 because we have 5 options.

So, the probability of a correct answer is:

`P(C)=(1)/(5)`

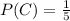
And for the probability of a wrong answer, since 4 of the 5 options are wrong:

`P(W)=(4)/(5)`

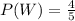
Now, we are asked for:

`P(CCW)`

So we need to use the multiplication rule to find this probability:

`P(CCW)=P(C)* P(C)* P(W)`

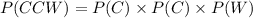
We substitute P(C) and P(W):

`P(CCW)=(1)/(5)*(1)/(5)*(4)/(5)`

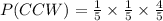
To make this multiplication, we multiply all the numerators and all of the denominators:

`\begin{gathered} P(CCW)=(1*1*4)/(5*5*5) \\ \\ P(CCW)=(4)/(125) \end{gathered}`

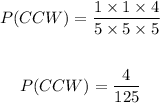
We can leave the answer as a fraction, or we can convert to a decimal:

`P(CCW)=(4)/(125)=0.032`

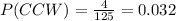
Answer:

`P(CCW)=(4)/(125)=0.032`