In order to find the value of the investment, we can use the following equation:
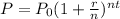
Where P is the final value, P0 is the initial value, r is the annual rate, t is the amount of time and n is a factor that depends on the compound interval (for a semiannual compound, we have n = 2).
So for the first period of 4 years, we have that:
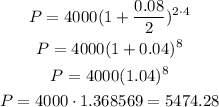
Then, we had an addition of 5000, so the new initial value is:
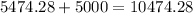
Now, for the next 2 years, we have that:

So the final value at the end of 6 years is $12,253.43