From the statement of the problem, we know that:
• Brian looks directly across and sees a pier,
,
• he walks downstream 400 ft, and looks at the pier again,
,
• he is now at an angle θ = 82°.
Using the data of the problem, we make the following diagram:
Where x is the distance across the river.
The diagram constitutes a triangle of:
• angle ,θ = 82°,,
,
• opposite side ,OC = 400 ft,,
,
• adjacent side ,AC = x,.
From trigonometry, we have the following trigonometric relation:
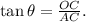
Replacing the data above in the last equation, we have:
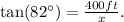
Solving for x the last equation, we find that:
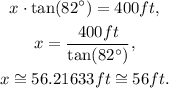
Answer
The distance across the river is approximately 56 ft.