Given:
m∠1 = (x² - 7x)
m∠7 = (-x + 7)
m∠1 and m∠7 are alternate exterior angles, and alternate exterior angles are congruent.
Therefore,
m∠1 = m∠7
(x² - 7x) = (-x + 7)
Let's solve for the values of x:
Move all the terms to the left hand side and equate to zero
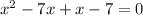
Let's factorize:
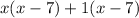
Now, the factors are:
(x + 1) and (x - 7)
Equate each factor to zero and solve for x:
x + 1 = 0
x = 0 - 1
x = -1
x - 7 = 0
x = 0 + 7
x = 7
Therefore, the values of x are:
-1 and 7
ANSWER:
x = -1 and 7