Answer:
17.33 years.
Step-by-step explanation:
The value of the property increases according to the equation:
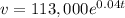
When the building is double its current value:
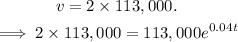
We want to solve for t:
Divide both sides by 113,000
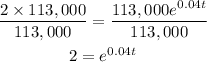
Take the natural logarithm (ln) of both sides:
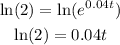
Finally, divide both sides by 0.04:
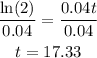
In 17.33 years, the value of the building will double its current value.