Solution
Let the number of adult tickets be A
Let the number of child's tickets be C
Since Amc sold 548 movie tickets.
A + C = 548 ------(1)
Also, if an adult’s ticket costs $13 and a child’s ticket costs $7 and the movie theater made $5762,
=> 13A + 7C = 5762 -----(2)
solving equations (1) and (2) simultaneously,

Substituting 548 - C for A in equation (2)
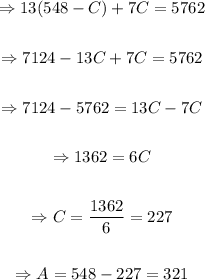
There are 321 adult tickets being sold and 227 children's tickets were sold.