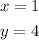Answer:
The solution to the system of equations is;
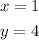
Step-by-step explanation:
Given the system of equation;
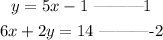
Let us solve by substitution;
substitute equation 1 to 2;
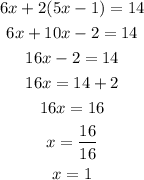
since we have the value of x, let us substitute into equation 1 to get the value of y;
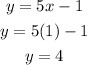
Therefore, the solution to the system of equations is;