We know that two mechanics worked on a car. The first mechanic charged $115 per hour, and the second mechanic charged $85 per hour. The mechanics worked for a combined total of 20 hours, and together they charged a total of $1850.
To find the answer we must represent the situation with a system of equations.
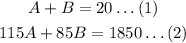
Where,
A: Number of hours that the first mechanic worked
B: Number of hours that the second mechanic worked
First, we must multiply equation 1 by -115
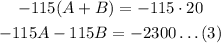
Second, we must add equations 2 and 3
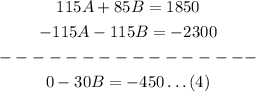
Now, we can solve equation 4 for B
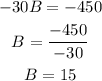
Then, we must replace the value of B in the equation 1 and finally we must solve for A
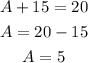
Answer:
First mechanic: 5 hours
Second mechanic: 15 hours