Question

Perimeter is 20cm. Can you find the missing side of the rectangle? Width is 6cm

Answer 1

The perimeter P of the rectagle is

`P=2W+2H`

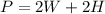
where W is the width and H the height.

By substituting the given values into the perimeter, we have

`20=2\cdot6+2\cdot H`

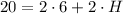
which is equal to

`20=12+2W`

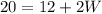
and we need to isolate W. This can be obtained by moving +12 to the left hand side as -12. It yields,

`\begin{gathered} 20-12=2W \\ 8=2W \end{gathered}`

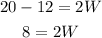
and finally, W is given by

`\begin{gathered} 2W=8 \\ W=(8)/(2) \\ W=4 \end{gathered}`

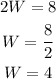
That is, each of the remaining sides measure 4 cm