In order to complete the square of a quadratic equation, first let's identify the notable product below: the square of a sum:
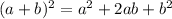
So, in order to complete the square of a quadratic expression ax² + bx + c, when a = 1, we can add and subtract the term (b/2)², this way we have:
![\begin{gathered} x^2+bx+c=0\\ \\ x^2+bx+((b)/(2))^2-((b)/(2))^2+c=0\\ \\ (x+(b)/(2))^2-((b)/(2))^2+c=0\\ \\ (x+(b)/(2))^2=((b)/(2))^2-c\\ \\ x+(b)/(2)=\pm\sqrt{((b)/(2))^2-c}\\ \\ x=-(b)/(2)\pm\sqrt{((b)/(2))^2-c}\\ \\ x=(-b\pm√(b^2-4c)\\)/(2) \end{gathered}]()
If a is not equal to 1, we can write the following general solution:
