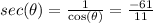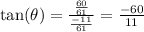So, here we have the point:
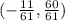
This is situated at the quadrant II.
Remember that sin(a) is a relation between the opposite side of the angle a and the hypotenuse of the triangle.
To find the hypotenuse, we apply the Pythagorean Theorem:
![\begin{gathered} h=\sqrt[]{((60)/(61))^2+((-11)/(61))^2} \\ h=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5j470qc32cevzzd9uhakrot8oq1naowl82.png)
Notice that as this point is in the unit circle, the hypotenuse is 1.
Now,
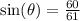
And,