Part A. We are given that the velocity function of a particle is given by:
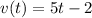
We are asked to determine the displacement. To do that we need to determine the formula for the distance. Let's remember that the distance is given by:
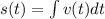
Now, we substitute the formula for the velocity:
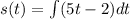
Now, we distribute the integral:
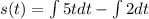
Now, we use the following formula for integration:
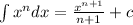
Applying the rule we get:
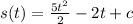
Now, to determine the displacement we need to determine the difference between the positions, like this:
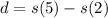
Now, we substitute the values in the formula for the position:
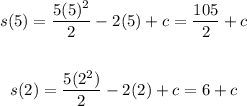
Now, we substitute in the formula for the displacement:
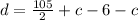
Solving the operations:
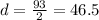
Therefore, the displacement is 46.5 minutes
Part B. The displacement of the particle between an initial time "t = 0" and a final time "t" is:
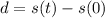
Substituting we get:
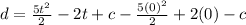
Solving the operations:
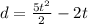
Now, we set the displacement to zero:
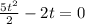
Now, we take "t" as a common factor:
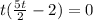
Since we want the value of time that is different from zero we set the second factor to zero:
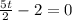
Now, we add 2 to both sides:
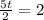
Now, we multiply both sides by 2:
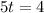
Now, we divide both sides by 5:
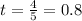
Therefore, the time is 0.8 minutes.