Answer:
Perpendicular.
Step-by-step explanation:
We will need to recall the basic definitions below:
• The slope-intercept form of the equation of a line is y=mx+b.
• Two lines are parallel if their slopes are the same.
,
• Two lines are perpendicular if the product of their slopes is -1.
Given the two lines:
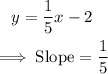
The second line:
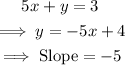
The product of the slopes:

Thus, the two lines are perpendicular.