Question

a catapult launches a boulder with an upward velocity of 148 ft the height of the boulder H in feet after T seconds is given by the function H equals negative 16 t squared + 148 t + 30 how long does it take the boulder to reach its maximum height what is the boulders maximum height round to the nearest hundredth if necessary

Answer 1

`h=-16t^2+148t+30\text{ }`

To get the time it takes the boulder to reach maximum height, we will have to use the relation: At maximum height, the velocity is Zero

Step 1: Let's get the velocity

To get the velocity, we will have to find the derivative of the function

`\frac{dh\text{ }}{dx}=-32t\text{ + 148}`

`\begin{gathered} velocity,\text{ v = }\frac{dh\text{ }}{dx}=-32t^{}\text{ + 148} \\ v\text{ }=-32t^{}\text{ + 148} \end{gathered}`

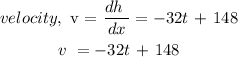
Step 2: Equate the velocity to zero

`\begin{gathered} v=0=-32t^{}\text{ + 148} \\ 0=-32t^{}\text{ + 148} \\ \\ 32t^{}\text{ = 148} \\ \end{gathered}`

Dividing both sides by 32

`\begin{gathered} t\text{ =}(148)/(32) \\ \\ t\text{ = 4.625 seconds} \\ \\ t\text{ = 4.63 seconds} \end{gathered}`

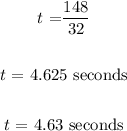
To obtain the maximum height, we will substitute t = 4.63 seconds into the equation

`\begin{gathered} h=-16t^2\text{ + 148t + 30} \\ put\text{ t = 4.63} \\ h\text{ = -16 x 4.63 x 4.63 + 148 x 4.63 + 30} \\ h=\text{ -342.99 + 685.24 + 30} \end{gathered}`

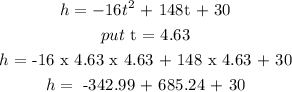
h = 372.25

So it means that a maximum height of 372.25 Ft is reached after 4.63 seconds

Option D is the answer