Question

Please help on any part you can. I know it is a lot but any help I’d greatly appreciate. I attempted the problem but still do not understand. Thank you so much!

Answer 1

A force diagram of the given situation is shown below:

As you can notice, tension force T and weight m*g of the object are opposite.

If the object goes downward with an acceleration 2m/s^2, it means that there is a net force, given by:

Fnet = m*g - T = m*a

m: mass of the obejct = 215 kg

a: acceleration = 2 m/s^2

g: gravitational acceleration constant = 9.8m/s^2

(a) Solve the equation above for T and replace the values of the other parameters:

T = m*g - m*a

T = (215kg)(9.8m/s^2) - (215kg)(2m/s^2)

T = 1677N

(b) The net work is given by:

Wnet = Wweight - Wtension

Wtension is the work done by the tension and Wweight is the work done by the weight of the object.

Wtension = T*y

Wweight = m*g*y

y is the vertical distance traveled by the object, which is y = 20m. Replace the values of m, g, y and T into the previous expressions:

Wtension = (1677N)(20m) = 33540J

Wweight = (215kg)(9.8m/s^2)(20m) = 42140J

Wnet = 42140J - 33540J = 8600J

(c) The work done by the cable is the work done by the tension:

Wcable = Wtension = 33540J

(d) Work done by gravity is the work done by the weight of the object:

Wgravity = Wweight = 42140J

(e) Use the following kinematic formula for the final speed of the obejct:

`v^2=v^2_o+2gy`

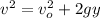
where,

vo: initial speed = 0m/s

v: final speed = ?

y: vertical distance = 20m

g: gravitational acceleration constant = 9.8m/s^2

Solve for v and replace the values of the other parameters and simplify:

`\begin{gathered} v=\sqrt[]{2gy} \\ v=\sqrt[]{2(9.8(m)/(s^2))(20m)} \\ v\approx19.80(m)/(s) \end{gathered}`