Let the two sides be represented by x,
Let the third side be 2x - 6 since it is 6m less than twice the common length.
The perimeter of the triangle is,
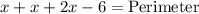
Given that the perimeter of the triangle is 10m, let us solve for x,
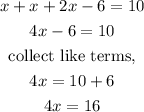
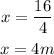
Let us now get the length of the three sides of the triangle,

Hence, the length of the three sides are 4m, 4m, and 2m.