Question

3x+2y+2z = -22x+y-z = -2x-3y+z = 0Solving for X, Y, and Z

Answer 1

You have a system of 3 equations with 3 unknown variables.

`\begin{gathered} 3x+2y+2z=-2\text{ (1)} \\ 2x+y-z=-2\text{ (2)} \\ x-3y+z=0\text{ (3)} \end{gathered}`

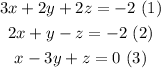
You can start by applying the reduction or elimination method to solve the system. Let's add equation (3) and equation (2)

`\begin{gathered} x-3y+z=0 \\ 2x+y-z=-2 \\ ------------ \\ 3x-2y+0=-2 \end{gathered}`

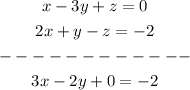
This will be equation (4).

Now, let's apply the same method to equation (1) and (2) but, first you need to multiply equation (2) by 2:

`\begin{gathered} 2(2x+y-z)=2(-2) \\ 4x+2y-2z=-4\text{ Eq. }(5) \end{gathered}`

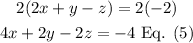
Add equation (1) and (5)

`\begin{gathered} 3x+2y+2z=-2 \\ 4x+2y-2z=-4 \\ -------------- \\ 7x+4y+0=-6 \end{gathered}`

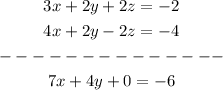
This will be equation (6).

Now, let's apply the elimination method again to equations (4) and (6). But, first let's multiply equation (4) by 2:

`\begin{gathered} 2(3x-2y)=2(-2) \\ 6x-4y=-4\text{ (7)} \end{gathered}`

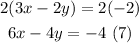
Now, let's add equations (6) and (7):

`\begin{gathered} 7x+4y=-6 \\ 6x-4y=-4 \\ ----------- \\ 13x+0=-10 \\ \text{Now let's solve for x} \\ 13x=-10 \\ \text{Divide both sides by 13} \\ x=-(10)/(13) \end{gathered}`

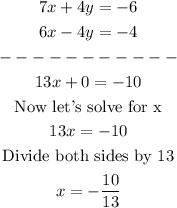
Now, you can replace this x-value into equation (6)

`\begin{gathered} 7x+4y=-6 \\ 7(-(10)/(13))+4y=-6 \\ -(70)/(13)+4y=-6 \\ 4y=-6+(70)/(13) \\ 4y=(-6*13+70)/(13)=(-78+70)/(13) \\ 4y=-(8)/(13) \\ \text{Divide both sides by 4} \\ (4y)/(4)=(-(8)/(13))/(4) \\ \text{Simplify} \\ y=-(8)/(13*4)=-(2)/(13) \end{gathered}`

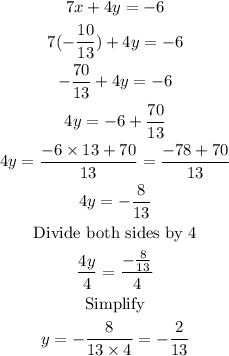
You know that x=-10/13, y=-2/13, now you can replace these values in any equation to find z-value:

Let's do it with equation (3)

`\begin{gathered} x-3y+z=0 \\ -(10)/(13)-3(-(2)/(13))+z=0 \\ -(10)/(13)+(6)/(13)+z=0 \\ -(4)/(13)+z=0 \\ z=(4)/(13) \end{gathered}`

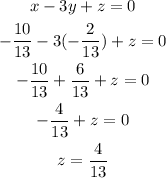
The answer is X=-10/13, Y=-2/13 and Z=4/13