We have the following system of inequalities:
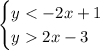
And we need to determine from a list of solutions which of them are solutions to the system of inequalities.
1. To find them, we can graph both lines, and we can graph them by finding their intercepts, the x- and the y-intercepts:
Line -2x + 1
The x-intercept is the point on the x-axis where y = 0. Then we have:
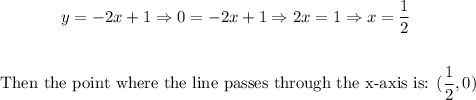
The y-intercept is the point of the line on the y-axis where x = 0. Then we have:
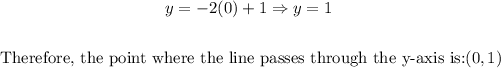
Then with these two points, (1/2, 0) and (0,1), we can graph the line of the inequality.
Line 2x-3
We can proceed in a similar way as before, to find the intercepts of this line:
The x-intercept:
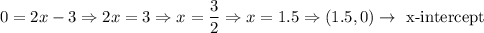
The y-intercept:
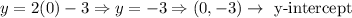
Then we can graph the line using the points (1.5, 0) and (0, -3).
2. Now, we can graph the lines using the obtained intercepts, and we have to find the shaded areas to represent the solutions to the inequality in each case:
• We can use a test point (0, 0), if the inequality y < -2x + 1 is satisfied, then (0,0) - and other points in this part of the area are solutions to this inequality. Then we have:
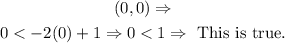
Then we can graph the first inequality as follows:
Notice that the line is represented by a dotted line since the solutions are for values LESS to (and not equal) to the line.
We can proceed in a similar way to find the graph of the other inequality, y > 2x - 3:
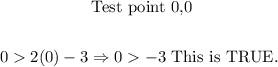
Then we can graph the inequality as follows:
3. Now we are ready to find the solutions to the two inequalities. We can draw both inequalities as follows:
And the violet area represents the area for the solutions to both inequalities.
4. Now, we can graph the given points of the list, and if one of them lies on the area, then the point is a solution to the system of inequalities:
Therefore, the solutions to the inequalities system are the points: (-3, 1) and (-2, -2) (Options A and E).