Answer:
x = -3/2 or x = 5/3
Step-by-step explanation:
Given:
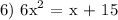
To find:
the value of x
First we need to re-write the given equation into the form ax² + bx + c = 0:
a = coefficient of x², b = coefficient of b and c = constant
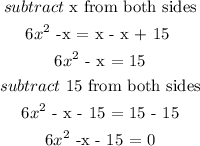
a = 6, b = -1, c = -15
Next we will find the factors of ac whose sum gives b
ac = a × c = 6 × -15 = -90
So we need to find factors of -90 whose sum will give -1
The factors are: -10 and 9
-10 × 9 = -90
-10 + 9 = -1
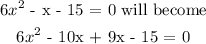

NB: when we factorise using factoring method, the numbers in both parenthesis will be the same
