Given:
The intial population in 2019 is, P₀ = 103126.
The final population in 2020 is, P = 103856.
The objective is to find the population in the year 2039.
Step-by-step explanation:
The general exponential form of population growth is,
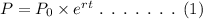
Here, t represents the time period.
To find t:
The value of t from 2019 to 2020 can be calculated as,
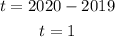
To find r :
On plugging the obtained values in equation (1),
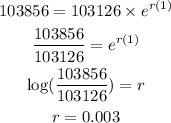
To find population at 2039:
The time period t can be calculated as,
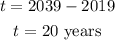
Now, final population after 2019 can be calculated as,
![undefined]()