Question

I am using Bay County, a county located in the state of Michigan. According to the U.S. Census Bay county had a population of 103,126 in 2019 and in 2020 it had 103,856. How much would it grow by 2039? How will I represent the growth assuming an exponential model? The picture attached is the excel I have to use. so if you have an equation to insert in a column just an equation that'll work!

Answer 1

Given:

The intial population in 2019 is, P₀ = 103126.

The final population in 2020 is, P = 103856.

The objective is to find the population in the year 2039.

Step-by-step explanation:

The general exponential form of population growth is,

`P=P_0* e^(rt)\text{ . . . . . . . (1)}`

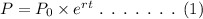
Here, t represents the time period.

To find t:

The value of t from 2019 to 2020 can be calculated as,

`\begin{gathered} t=2020-2019 \\ t=1 \end{gathered}`

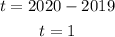
To find r :

On plugging the obtained values in equation (1),

`\begin{gathered} 103856=103126* e^(r(1)) \\ (103856)/(103126)=e^(r(1)) \\ \log ((103856)/(103126))=r \\ r=0.003 \end{gathered}`

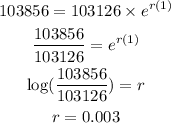
To find population at 2039:

The time period t can be calculated as,

`\begin{gathered} t=2039-2019 \\ t=20\text{ years} \end{gathered}`

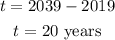
Now, final population after 2019 can be calculated as,