We will have the following:
In order to determine the number of years from the time of introduction in which the population would double, we will proceed as follows:
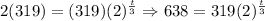
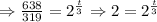
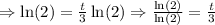
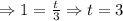
So, the number of years it would take for the population of alligators to double would be 3 years.