Question

If the diameter of a circle is segment AB where Point A is located at (-3, 6), and Point B located at (-8, -1), what is the diameter of the circle?

Answer 1

√74 units.

Explanation:

Given that segment AB is the diameter of the circle and the points A and B are located at:

`\begin{gathered} (x_1,y_1)=A(-3,6) \\ \left(x_2,y_2\right)=B\left(-8,-1\right) \end{gathered}`

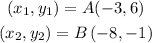
The diameter of the circle is the length of segment AB.

To find the length of the segment, we use the distance formula given below:

`$$Distance=√((x_2-x_1)^2+(y_2-y_1)^2) $$`

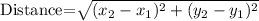
Substitute the given values:

`\begin{gathered} AB=√((-8-\left(-3\right))^2+(-1-6)^2) \\ =√((-8+3\rparen^2+(7)^2) \\ =√(\lparen-5)^2+7^2) \\ =√(25+49) \\ \implies AB=√(74) \end{gathered}`

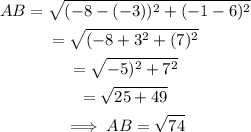
The diameter of the circle is √74 units.

The last option is correct.