Continuity of a Function
Given the function:
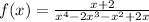
It's required to select one of the intervals for continuity.
To analyze the function's continuity, we need to factorize the denominator as follows:
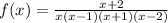
The denominator cannot be zero, thus each root of the polynomial in the denominator is a point of discontinuity. Listing them from least to greatest:
x = -1, x = 0, x = 1, x = 2
Any interval that contains one or more of the above-listed points is not an interval of continuity. Let's analyze them:
A. [-2.5, -1.5]
Both endpoints lie to the left of x = -1, thus the function is continuous in the interval
B. [-1.5, -0.5]
This interval contains the point x = -1, thus the function is not continuous here.
C. [-0.5, 0.5]
This interval contains the point x = 0, thus the function is not continuous here.
D. [1.5, 2.5]
This interval contains the point x = 2, thus the function is not continuous here.
Answer: A. [-2.5, -1.5]