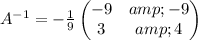Remember the following rule to find the inverse of a 2x2 matrix:
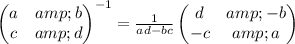
And it is well defined whenever ad-bc is different from 0.
The system of equations can be written as a product of a matrix A and a vector (x,y) as:
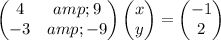
The system can be solved by multiplying both members by the inverse of the matrix (4 9 \\ -3 -9):
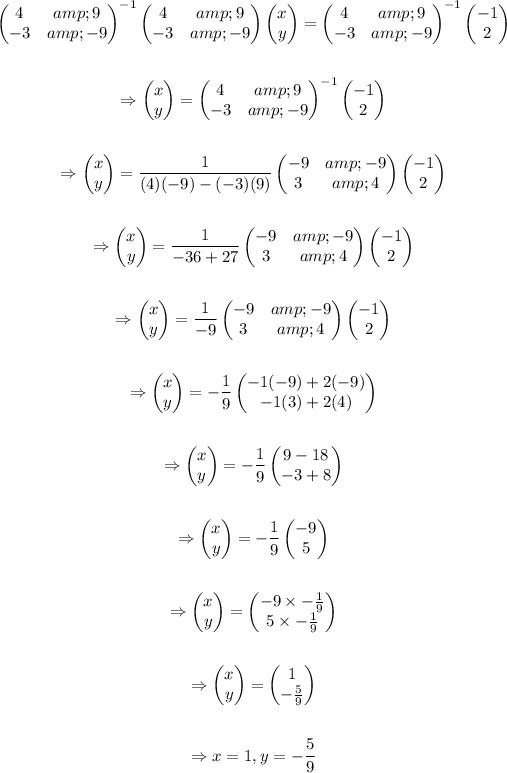
Therefore, the inverse matrix used to solve the system is: