Question

Let f(x) = X-2 and g(x) = x^2. Find the value of (gof)(4).A.14B.4C.62D.32

Answer 1

Answer: B.4

Step-by-step explanation:

We have the following fucntions:

`\begin{gathered} f(x)=x-2 \\ g(x)=x^2 \end{gathered}`

We need to find the composition:

`(g\circ f)(4)`

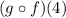
For this, first we need to find:

`(g\circ f)(x)`

Which by the definition of composition of functions is:

`(g\circ f)(x)=g(f(x))`

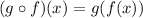
So we need to substitute f(x), in the x of g(x), as follows:

`(g\circ f)(x)=g(f(x))=(x-2)^2`

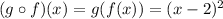
This is because of how f(x) and g(x) are defined in the problem.

Now, we find what we are asked for:

`(g\circ f)(4)`

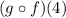
we are going to need to substitute the value of x=4 into what we found for (gof)(x):

`\begin{gathered} (g\circ f)(4)=(4-2)^2 \\ (g\circ f)(4)=(2)^2 \\ (g\circ f)(4)=4 \end{gathered}`

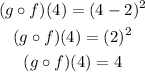
The answer is B.4