The annually compounded interest formula is:
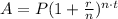
Where A is the amount you will have, P is the principal, r is the annual interest rate expressed as a decimal, n is the number of times the interest is compounded per time period (in this case as it is compounded annually, n=1) and t is the amount of time (in years) that the money is saved.
Then, we know that:
A=$8000
P=$4200
r=6.75%/100%=0.0675
n=1
t=?
Replace the known values and then solve for t as follows:

Therefore, it will take 10 years to accumulate $8000 or more in the account.