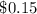The probability of selecting face card (jack,queen or king) is
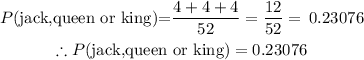
The probability of not selecting a face card (jack,queen or king):
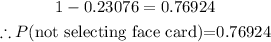
Therefore,
a) Kyd's Expected value is
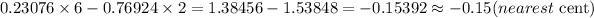
Hence, Kyd's Expected value is
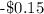
b) North's expected value is
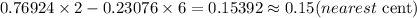
Hence, North's Expected value is