Question

A family buys a car for $20,000 the value of the car decreases about 18% each year after six years the family wants to sell the car should they sell the car for $4000 explain

Answer 1

Given in the question:

a.) A family buys a car for $20,000.

b.) The value of the car decreases about 18% each year.

c.) After six years the family wants to sell the car.

Should they sell the car for $4000?

Let's determine if the price of the car fits the recommended price using the formula below:

`\text{ y = }Ad^{x^{}}`

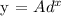
Where,

y = the recommended price of the car after 6 years.

A = price of the car when bought

d = (100% - 18%)/100 = 82/100 = 0.82

x = years of use

We get,

`\text{ y = }Ad^{x^{}}`
`\text{ y = (\$20,000)(0.82)}^{6^{}}`
`\text{= (\$20,000)(0}.30400667142)`
`\text{ y =\$}6,080.13342848\text{ }\approx\text{ \$6,080.13}`

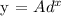
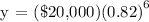
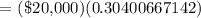
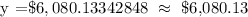
The computed depreciated value of the car is $6,080.13.

Therefore, we recommend that they should sell the car at a higher price but not more than $6,080.13 since it's still within the recommended depreciated value.