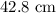Question

Consider the triangle shown below where m∠B=79∘, a=35.2 cm, and c=31.9 cm.Use the Law of Cosines to determine the value of x (the length of AC in cm).x=

Answer 1

The length of x is;

`42.8\text{ cm}`

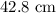
Step-by-step explanation:

Given the figure in the attached image;

The length of the sides and angle of the triangle are give as;

`\begin{gathered} a=35.2\text{ cm} \\ c=31.9\text{ cm} \\ m\angle B=79^(\circ) \end{gathered}`

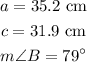
Recall that the law of cosines can be expressed as;

`c^2=a^2+b^2-2ab\cos C`

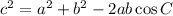
Since in this case we want to calculate b=AC=x;

`\begin{gathered} b^2=a^2+c^2-2ac\cos B \\ b=\sqrt[]{a^2+c^2-2ac\cos B} \\ x=\sqrt[]{a^2+c^2-2ac\cos B} \end{gathered}`

Substituting the given values;

`\begin{gathered} x=\sqrt[]{a^2+c^2-2ac\cos B} \\ x=\sqrt[]{35.2^2+31.9^2-2(35.2)(31.9)\cos 79^(\circ)} \\ x=\sqrt[]{35.2^2+31.9^2-2(35.2)(31.9)\cos79^(\circ)} \\ x=\sqrt[]{1828.1387905} \\ x=42.7567 \\ x=42.8\text{ cm} \end{gathered}`

Therefore, the length of x is;

`42.8\text{ cm}`