First, we are going to plot the segment AB as:
Then, to find the coordinates that divide AB into 2 parts, we need to find the distance in the x-coordinate and the distance in the y-cordinate from points B to A as:
Distance x-coordinate = 5 - (- 10) = 5 + 10 = 15
Distance y-coordinate = 4 - (-6) = 4 + 6 = 10
So, we can calculate the distance from B to the partition points using the ratio as:
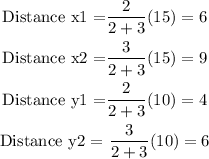
So, the coordinates of points C and D can be calculated as:
C = B + (distance x1, distance y1)
D = B + (distance x2, distance y2)
Replacing, we get:
C = (-10, -6) + (6, 4) = (-10+6, -6 + 4) = (-4, -2)
D = (-10, -6) + (9, 6) = (-10+9, -6 + 6) = (-1, 0)
Answer: C(-4, -2)
D(-1, 0)