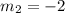Question

Two lines are perpendicular If one line has a slope of 1/2 what is the slope of the other line ?

Answer 1

The slope of the other line is;

`m_2=-2`

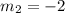
Step-by-step explanation:

Given that the two lines are perpendicular to each other and the slope of one line is;

`m_1=(1)/(2)_{}_{}`

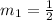
Recall that when two lines are perpendicular their slopes are negative reciprocal of each other;

`\begin{gathered} m_1m_2=-1 \\ m_2=-(1)/(m_1) \end{gathered}`

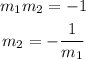
Substituting the given values;

`\begin{gathered} m_2=-(1)/(m_1)=(-1)/(((1)/(2))) \\ m_2=-(2)/(1) \\ m_2=-2 \end{gathered}`

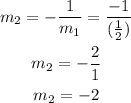
Therefore, the slope of the other line is;

`m_2=-2`