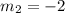Answer:
The slope of the other line is;
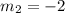
Step-by-step explanation:
Given that the two lines are perpendicular to each other and the slope of one line is;
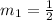
Recall that when two lines are perpendicular their slopes are negative reciprocal of each other;
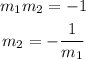
Substituting the given values;
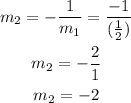
Therefore, the slope of the other line is;