We have the relationship between two variables that can be modeled by a line equation. We need first to determine the equation of the line. To do that can use the following equation for a line:

Where "m" is the slope and b the y-intercept. To determine the slope "m" we use the following formula:

Taking two points in the line:
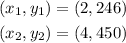
Replacing in the formula for the slope:
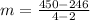
Solving the operations:
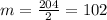
replacing in the equation for the line:
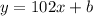
To find the value of "b" we replace any point through which the line passes. Replacing (x,y) = (2,246):
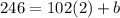
Solving the product:
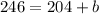
subtracting 204 to both sides:
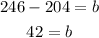
Replacing in the line equation:

The processing fee would be the initial fee and in the line equation, it is equivalent to the y-intercept therefore, the processing fee is $42. The daily fee is equivalent to the slope of the line, therefore, the daily fee is $102 per day.
If the total amount to spend is $1200 then replacing in the line equation:
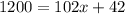
Solving for "x" first by subtracting 42 to both sides:
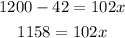
Dividing both sides by 102:

Therefore, the number of days is 11.4.