The given function is
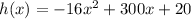
According to this function, the starting height of the rocket is 20 feet because that's the initial condition of the problem stated by the independent term.
Additionally, we find the maximum height by calculating the vertex of the function V(h,k).
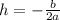
Where a = -16 and b = 300.
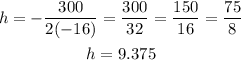
Then, we find k by evaluating the function
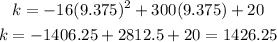
Hence, the maximum height is 1426.25 feet.
At last, to know the time need to hit the ground, we just use h=9.375 and we multiply it by 2
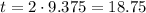
Hence, the rocket hits the ground after 18.75 seconds.